https://leetcode.com/problems/trapping-rain-water/description/
Trapping Rain Water - LeetCode
Can you solve this real interview question? Trapping Rain Water - Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining. Example 1: [https://assets.leetcode.com/upl
leetcode.com
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.
➡️ 입력 예제
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Input: height = [4,2,0,3,2,5]
Output: 9
❓ 문제 접근
이 문제는 빗물이 고인 합을 구하는 문제다.
빗물이 고이기 위해서는 진행되는 방향에서 현재 높이가 이전 높이보다 높아야 한다.
말은 어렵지만 그림으로 그려서 보면 이해가 쉽다.
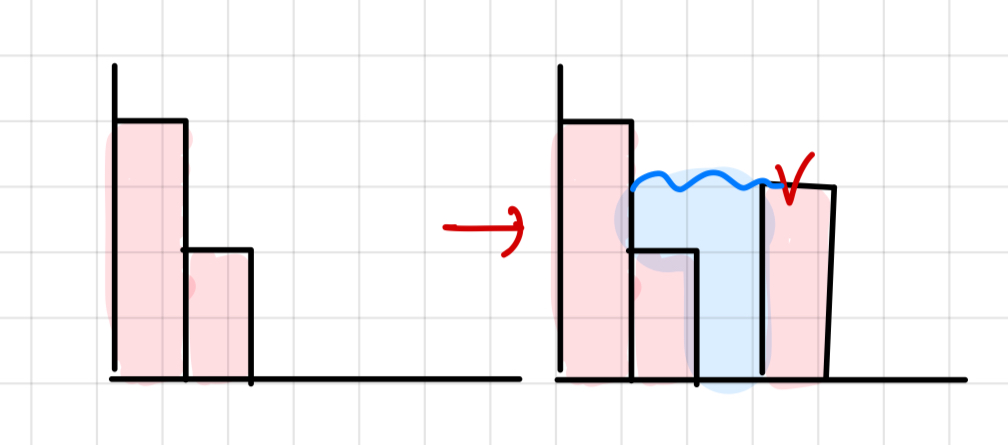
이대로 주어진input에 따라 그림 그려보면 이렇게 고인 물의 값을 알 수 있다.
모두 더하면 9가 나온다.
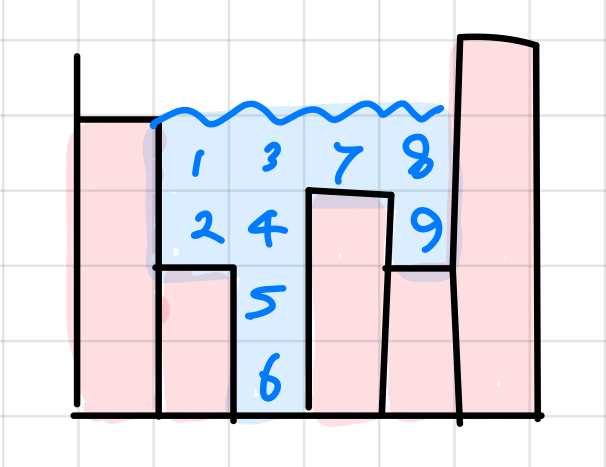
현재 바의 높이가 이전 바의 높이보다 높아지는 때를 변곡점으로 부르겠다.
왼쪽이서 오른쪽으로 for문 돌며 모든 숫자를 탐색할 거고
만약 변곡점을 만났다면 이전의 바의 높이를 다시 탐색하며 부피를 구해 더해가겠다.
✅ 풀이
1. for문 돌며 모든 숫자 탐색
2. 이전 바가 없다면 일단 쌓기
3. 현재 바의 높이가 이전 바의 높이보다 높다면 (변곡점) 이전에 부터 고인 물의 양 구하기
- 거리 = 현재 위치 - 변곡점 만나기 전 위치 - 1
- 물의 높이 = 현재 바의 높이와 이전 바의 높이 중 작은 값에서 변곡점을 만나는 위치의 높이를 뺀 값
- 부피 = 거리 * 물의 높이
4. 현재 바의 높이보다 높은 바를 만난다면 위치 변경
✨ 코드
class Solution {
public int trap(int[] nums) {
Deque<Integer> stack = new ArrayDeque<>();
int volumne = 0;
for (int i = 0; i < nums.length; i++) {
while(!stack.isEmpty() && nums[i] > nums[stack.peek()]) {
int top = stack.pop();
if (stack.isEmpty()) break;
int distance = i - stack.peek() - 1;
int waters = Math.min(nums[i], nums[stack.peek()]) - nums[top];
volumne += distance * waters;
}
stack.push(i);
}
return volumne;
}
}
💡 KeyPoint
peek() : 스택의 맨 위에 있는 요소(스택의 맨 위에 있는 요소를 제거하지 않고 가져오는 메서드)를 반환
pop() : 스택의 맨 위에 있는 요소를 제거해서 가져와 반환
참고
https://ebook-product.kyobobook.co.kr/dig/epd/ebook/E000005441444
자바 알고리즘 인터뷰 with 코틀린 | 박상길 | 책만- 교보ebook
[이 책의 구성] [1부] ‘코딩 인터뷰를 준비하며’ 1장 ‘코딩 인터뷰 & 코딩 테스트’에서는 각각에 대한 소개와 어떻게 하면 시험을 잘 치를 수 있을지, 문제 풀이 외에도 타임아웃이나 예외 처
ebook-product.kyobobook.co.kr
코드
https://github.com/recordbuffer/Coding_Test/tree/main/Java_Algorithm
'JAVA' 카테고리의 다른 글
| Leetcode 문자열 819 Most Common Word (java) (0) | 2023.11.14 |
|---|---|
| 백준 단계별로 풀기 자바 [5단계 - 1차원 배열] (1) | 2021.08.20 |
| 백준 단계별로 풀기 자바 [4단계 - while문] (0) | 2021.08.19 |
| 백준 단계별로 풀기 자바 [3단계 - for문] (0) | 2021.08.16 |
| 백준 단계별로 풀기 자바 [2단계 - if문] (1) | 2021.08.16 |



댓글